Fünfeck zeichnen und Fünfpass konstruieren

Arbeitsblatt und Kontruktionshinweise

Über das Fünfeck / Pentagramm / Fünfpass

Wie nennt man ein Fünfeck auch noch? Ein regelmäßiges Fünfeeck nennt man Pentagramm!

Ein Pentagramm hat somit 5 Seiten, falls dich jemand einmal fragen sollte: "Wie viele Seiten hat ein Pentagramm?"

Ein regelmäßiges Fünfeck hat fünf gleiche Innenwinkel von jeweils 108°.Dabei wendet man die Regel zur Berechnung der Summe der Innenwinkel im N Eck an. Stelle dir ein Quadrat oder Rechteck als spezielles Viereck vor. Dann können wir durch das Anlegen eines Dreiecks an einer Seite daraus ein Fünfeck machen. Das Dreieck fügt nun zur Summe der Innenwinkel von 360° noch weitere 180° hinzu. Das Fünfeck hat somit eine Winkelsumme von 540° (360° + 180°). Diese Regel kann man für jedes weitere N Eck anwenden, indem man für jede weitere Ecke IMMER 180° hinzufügt!

Die Konstruktion des Fünfeck birgt besondere Herausforderungen. In den Seiten des Fünfecks wie des Pentagramms taucht das Verhältnis des sog. Goldenen Schnitts auf. Diesen behandeln wir bald in einem eigenen Beitrag.

Auf dieser Seite wollen wir mit Arbeitsblättern oder auch einfach nur Malvorlagen den Zugang zum Fünfeck fördern und vor allem die Konstruktion alleine mit Zirkel und Lineal vorstellen.

Fünfpass

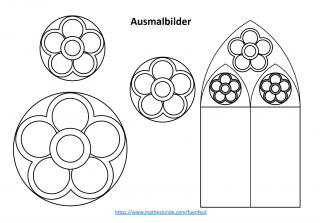
Als Vielpass (und dazu gehört auch der hier vorgestellte Fünfpass) werden in der Architektur gezackte runde oder halbrunde Zierformen bezeichnet, die vor allem in mittelalterlichen Bauwerken auftreten. Die hier beschreibenen Fünfpass Muster mit Kreisbögen finden wir insbesondere in Kirchenfenstern wieder, aber auch in aktuellen Bauwerken, wie dem Pentagon (griech. für Fünfeck).

Spitzbogenfenster mit Fünfpasselement (siehe Ausmalvorlage oder Konstruktion mit Powerpoint!)

Hinweise zu diesen Arbeitsblättern "Fünfeck"

Alle Zeichnungen wurden mit Powerpoint erstellt.Für die/den interessierte/n Schüler/in kann es eine zusätzliche Herausforderung sein, die Zeichnungen ebenfalls in Powerpoint nachzuvollziehen.

Dieses Thema ist konzipiert als ein Teil einer Reihe "Stationenlernen - Zirkelübungen - Vielecke". Dies kann bereits in den Klassen 4 bis 6 durchgeführt werden, da es sich um reine Konstruktionsaufgaben handelt, die keinerlei rechnerische Kenntnisse erfordern.

Dabei bildet diese Station eine der schwierigeren Stationen, da die Konstruktion des Fünfecks mit Zirkel und Lineal nicht einfach ist. Das Thema "Fünfeck, Pentagramm, Fünfpass" ist für besonders leistungsfähige Schüler gedacht, wenn die Stationen in der Klassenstufe 5 oder 6 durchgeführt werden. In der Klassenstufe 7/8/9 kann dieses Thema als Einstieg in Berechnungen mit Hilfe der Satzgruppe des Pythagoras und der Trigonometrie herangezogen werden.

Als einfachere Stationen haben wir die Themen "Vierpass" oder ganz einfach: das "Yin und Yang Symbol".

Die einzelnen Konstruktionsschritte eines Fünfecks

Schritt 1:

Zeichne eine waggerechte Line der Länge a = 10 cm am unteren Blattrand. Zeichne jetzt jeweils einen Kreis-bogen mit dem Radius r = 10 cm an den beiden Endpunkten A und B ein.

Schritt 2:

Nun zeichne eine Senkrechte Linie auf den linken Endpunkt der Strecke. (Ohne Geodreieck kann diese Senkrechte als Mittelsenkrechte konstruiert werden). Markiere den Schnittpunkt C dieser Senkrechten mit dem Kreisbogen.

Schritt 3:

Zeichne jetzt einen Kreisbogen mit dem Mittelpunkt in D (Mitte zwischen A und B) und dem Radius bis zu C. Hierbei ist es wichtig, die Strecke AB über A hinaus zu verlängern um den Schnittpunkt E zu erhalten.

Schritt 4:

Nun zeichne einen weiteren Kreisbogen mit dem Mittelpunkt in B und dem Radius bis zum Punkt E. Wir erhalten den Schnittpunkt F.

Schritt 5:

Verbinde den Punkt A mit dem Punkt F. Diese Strecke hat die Länge a = 10 cm und ist die zweite Seitenlänge unseres Fünfecks.

Schritt 6:

Nun schlagen wir vom Punkt F einen weiteren Kreisbogen mit dem gleichen Radius und wir erhalten den Schnittpunkt G mit der Mittelsenkrechten von A und B.

Schritt 7:

Von G aus zeichnen wir noch einen Kreisbogen mit dem gleichen Radius und wir erhalten den Schnittpunkt H.

Schritt 8:

Im letzten Schritt verbinden wir Punkt H mit B. Das Fünfeck (Pentagon) ist fertig gestellt.

Schritt 9 - Pentagramm:

Verbinden wir die gegenüber liegenden Ecken des Fünfecks, erhalten wir im Innern des Fünfecks einen fünfzackigen Stern, das Pentagramm!

Schritt 10 - Mittelpunkt:

Durch die Spitzen der gleichschenkligen Dreiecke die entstehen kann jeweils eine Senkrechte auf die gegenüber liegende Seite gezogen werden. Dadurch erhalten wir zusätzlich den Mittelpunkt des Fünfecks.