Vektorrechnung: Aufgaben und Beispiele für das Abitur
Einführung in die Vektorrechnung
Die Vektorrechnung ist ein zentraler Bestandteil der Mathematik im Abitur. Sie wird vor allem in der Geometrie und der linearen Algebra angewendet. Vektoren beschreiben sowohl Richtungen als auch Größen und sind unverzichtbar für das Verständnis von Ebenen, Geraden und deren Beziehungen.
Grundlagen: Vektoraddition und -subtraktion
Die Addition und Subtraktion von Vektoren erfolgt komponentenweise. Beispielsweise ergibt die Addition der Vektoren a = (2, 3) und b = (4, -1) den Vektor a + b = (6, 2). Solche Aufgaben sind essenziell für die Grundlagen der Vektorrechnung.
Das Skalarprodukt und seine Anwendungen
Das Skalarprodukt zweier Vektoren wird berechnet, indem die entsprechenden Komponenten multipliziert und die Ergebnisse addiert werden. Es dient zur Berechnung von Winkeln zwischen Vektoren und ist eine wichtige Grundlage für orthogonale Projektionen.
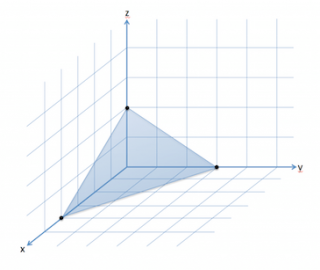
Parameterdarstellung von Geraden und Ebenen
Mit Vektoren lassen sich Geraden und Ebenen in der Geometrie darstellen. Eine Gerade wird durch einen Stützvektor und einen Richtungsvektor beschrieben, während eine Ebene drei Parameter benötigt. Solche Darstellungen sind wichtig für das Lösen geometrischer Probleme.
Praktische Aufgaben zur Vorbereitung
Zur Vorbereitung auf das Abitur sollten Sie verschiedene Aufgaben lösen, wie:
- Berechnung des Winkels zwischen zwei Vektoren mit dem Skalarprodukt.
- Bestimmung von Schnittpunkten zwischen Geraden und Ebenen.
- Untersuchung, ob zwei Vektoren linear unabhängig sind.
Weitere Übungsaufgaben finden Sie auf Webseiten wie Mathefritz.com oder Mathestunde.com.