Wie sieht ein 90 Grad Winkel aus?
Ein 90 Grad Winkel, auch als rechter Winkel bezeichnet, ist ein Winkel, der zwei Linien so verbindet, dass sie sich in einem Quadrat oder Rechteck rechtwinklig gegenüberstehen. Er bildet eine exakte L-Form und wird in der Geometrie oft verwendet, um die Form und Symmetrie von Objekten zu definieren.
Was ist ein 90 Grad Winkel?
Ein 90-Grad-Winkel ist ein Winkel, der aus zwei Linien besteht, die sich exakt im rechten Winkel schneiden. In der Mathematik und Geometrie schreibt man den rechten Winkel meist als:
\[ \angle = 90^\circ \]
Dieser Winkel wird oft in Quadraten, Rechtecken und vielen anderen Formen verwendet, die Symmetrie und Stabilität erfordern.
Darstellung eines 90-Grad-Winkels
Ein 90-Grad-Winkel sieht so aus, dass eine Linie vertikal und die andere Linie horizontal verläuft und sie sich genau an einem Punkt schneiden, sodass die beiden Linien einen „rechten Winkel“ bilden.
Beispiele für 90 Grad Winkel
In der realen Welt gibt es viele Beispiele für 90 Grad Winkel, darunter:
- Die Ecken eines Quadrats oder Rechtecks
- Die Verbindungspunkte in einem Kreuzworträtsel
- Die Positionen von Straßenkreuzungen, bei denen Straßen rechtwinklig aufeinandertreffen
Warum ist ein 90 Grad Winkel wichtig?
90° Winkel sind in der Mathematik und im Alltag sehr wichtig, da sie Symmetrie und Stabilität bieten. Zum Beispiel hat jedes Gebäude rechte Winkel, damit es stabil und symmetrisch bleibt. Auch im Handwerk und in der Technik ist der rechte Winkel von großer Bedeutung.
Warum ist das Messen, Zeichnen und Bestimmen von Winkeln so wichtig?
Beim Messen und Zeichnen von Winkeln sind einige grundlegende Punkte wichtig, um präzise Ergebnisse zu erzielen:
1. Verwendung eines Geodreiecks oder Winkelmessers
- Geodreieck: Ein Geodreieck ist das häufigste Werkzeug, um Winkel zu messen und zu zeichnen. Es hat eine Skala, die es ermöglicht, Winkel von 0° bis 180° abzulesen.
- Winkelmesser: Wenn der Winkel größer als 180° ist, kommt oft ein Winkelmesser zum Einsatz, der 360° abdeckt.
2. Startpunkt bestimmen
- Der Winkel wird immer vom Scheitelpunkt (dem Punkt, an dem die beiden Schenkel des Winkels aufeinandertreffen) aus gemessen. Dieser Punkt sollte genau auf der 0-Marke des Geodreiecks oder Winkelmessers liegen.
3. Richtige Ausrichtung
- Der Nullpunkt des Geodreiecks muss genau auf einem der beiden Schenkel des Winkels liegen. Dann wird entlang der Skala der Wert des Winkels abgelesen.
4. Zeichnen von Winkeln
- Um einen Winkel zu zeichnen, legst du einen Schenkel des Winkels entlang der 0°-Linie des Geodreiecks. Dann markierst du den Punkt, der dem gewünschten Winkel entspricht, und ziehst von dort aus den zweiten Schenkel durch den Scheitelpunkt.
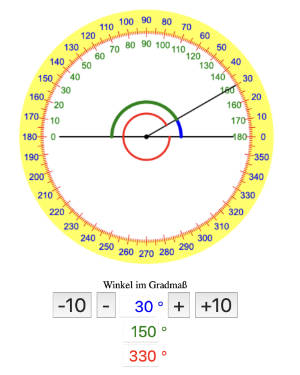
Wichtig Winkel: 30 Grad Winkel messen - Einfach in unserer Winkel-App nachprüfen!
Der blau eingezeichnete Winkel ist der 30 Grad Winkel!
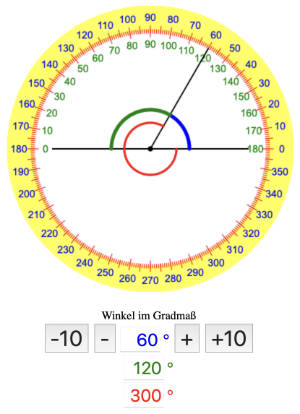
Wichtig Winkel: 60 Grad Winkel messen - Einfach in unserer Winkel-App nachprüfen!
Der blau eingezeichnete Winkel ist der 60 Grad Winkel!
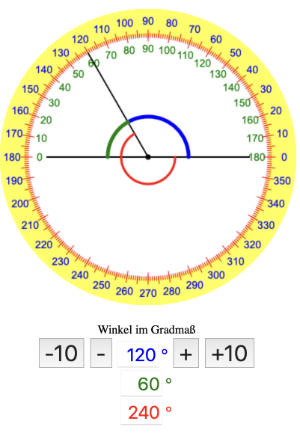
Wichtig Winkel: 120 Grad Winkel messen - Einfach in unserer Winkel-App nachprüfen!
Der blau eingezeichnete Winkel ist der 120 Grad Winkel!
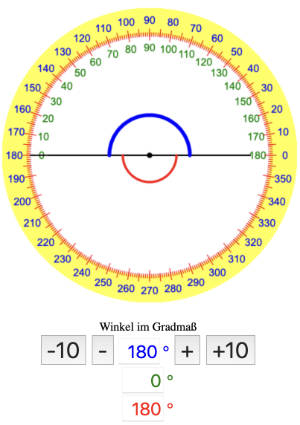
Wichtig Winkel: 180 Grad Winkel messen - Einfach in unserer Winkel-App nachprüfen!
Der blau eingezeichnete Winkel ist der 180 Grad Winkel!
Wichtig Winkel: 270 Grad Winkel messen - Einfach in unserer Winkel-App nachprüfen!
Der blau eingezeichnete Winkel ist der 270 Grad Winkel!
Wo wird das gebraucht?
1. Geometrie und Mathematik:
- In der Schule ist das Messen und Zeichnen von Winkeln ein zentraler Bestandteil des Geometrieunterrichts. Es ist wichtig für das Verständnis von Formen wie Dreiecken, Vierecken und Kreisen.
2. Bau und Architektur:
- Beim Entwerfen von Gebäuden und Strukturen ist das genaue Messen und Zeichnen von Winkeln entscheidend, um stabile und sichere Konstruktionen zu gewährleisten.
3. Technisches Zeichnen:
- In vielen technischen Berufen, wie im Maschinenbau oder der Elektrotechnik, ist präzises Arbeiten mit Winkeln notwendig, um Bauteile korrekt zu planen.
4. Astronomie und Physik:
- In der Astronomie misst man Winkel, um die Position von Sternen und Planeten zu bestimmen. In der Physik ist das Arbeiten mit Winkeln z.B. in der Optik oder Mechanik wichtig.
5. Kunst und Design:
- Auch im Bereich der Gestaltung, etwa beim Zeichnen von Perspektiven oder Mustern, spielen Winkel eine Rolle.
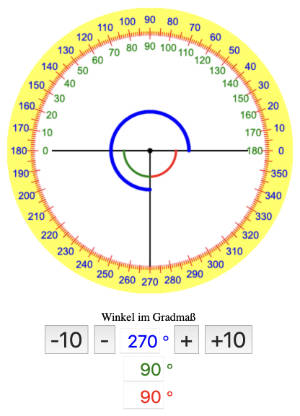
In dieser interaktiven Winkel App kannst du alle Winkel von 0° bis 360° online prüfen und dir anzeigen lassen. Zu jedem Winkel werden die Ergänzungswinkel zu 180° und zu 360° in verschiedenen Farben angezeigt. Probiere es aus. Du kannst den Winkel in Schritten zu 1° oder 10° verändern.Winkel lernen und Winkel online prüfen mit unserer Winkel App
Winkel im Gradmaß
°
°
°
In den beiden Lernvideos zu Winkel messen und Winkel zeichnen lernst du sehr schnell, wie man richtig Winkel ausmisst und Winkel zeichnet. Das Zeichnen und Messen von Winkeln ist sehr wichtig, nicht nur in der Mathematik, sondern auch zum Beispiel in der Physik beim Reflexionsgesetz und beim Brechnungsgesetz.Winkel messen und Winkel zeichnen - Lernvideos von Mathefritz
https://mathestunde.com/winkel-messen // https://mathestunde.com/winkel-zeichnen https://www.mathestunde.com/wie-sieht-ein-45-grad-winkel-aus https://www.mathestunde.com/wie-sieht-ein-90-grad-winkel-aus Weitere Infos und Seiten bei Mathestunde.com zum Thema Winkel
Übungsaufgaben
Versuche folgende Übungsaufgaben, um dein Wissen über 90-Grad-Winkel zu testen:
- Zeichne auf einem Blatt Papier einen 90 ° Winkel.
- Finde im Raum oder im Freien Beispiele für 90° Winkel (z. B. Türrahmen, Fensterrahmen).
- Überlege dir, warum ein 90 Grad Winkel auch als rechter Winkel bezeichnet wird.

