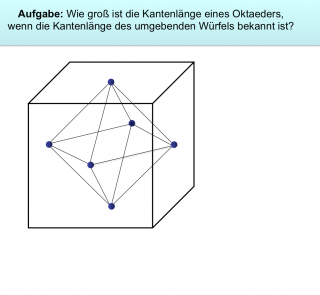
Klassische Aufgabe zur Satzgruppe des Pythagoras:
Berechne die Kantenlänge eines Oktaeders aus dem umschließenden Würfel.

So entsteht ein Oktaeder:
Ein Oktaeder besteht aus 8 gleichseitigen Dreiecksflächen. Diese entstehen, wenn man die Mitten eines Würfels miteinander verbindet.
Wenn die Kantenlänge des Würfels bekannt ist, kann man die Kantenlänge des Oktaeders mit Hilfe des Satzes von Pythagoras bestimmen.
Den Oktaeder zeichnet man, indem man zunächst einen Würfel zeichnet und anschließend auf jeder Würfelfläche (6 Quadrate) zwei Diagonalen zeichnet. Der Schnittpunkt der Diagonalen ist die Ecke des Oktaeders.
Powerpoint Datei: Oktaeder mit Hilfe von Pythagoras berechnen.
Ich habe euch eine Powerpoint-Datei zum Download bereit gestellt.


Video mit Musterlösung
Hinweis: im Video wurde das Seitenverhältnis beim Hochladen und Einstellen auf HD verzerrt und dadurch erscheint der Würfel und das Quadrat nicht mehr ganz so wie es aussehen sollte.