Einführung von Rechtecksummen zur Annhäherung des Flächeninhalts unter einem Graphen
Archimedes (287 v.Chr. - 212 v.Chr.) führte zur Bestimmung des Flächeninhalts eines Parabelsegments die sog. Streifenmehthode ein.
Anstelle von Streifen sprechen wir heute von Rechtecksummen oder auch Obersummen und Untersummen.
Mit Hilfe eines Arbeitsblatts wollen wir die Ober- und Untersummen einzeichnen und für das Intervall von (0;1) Schritt für Schritt berechnen.
Hierzu wurden folgende Funktionen ausgewählt:
1. eine lineare Funktion, die Ursprungsgerade mit der Steigung 1: f(x) = x
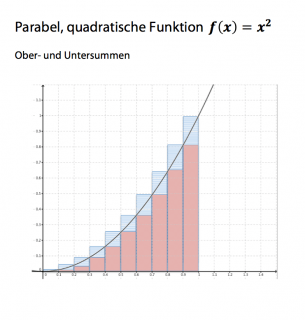
2. die Normalparabel f(x) = x^2
Arbeitsblatt mit proportionaler Funktion und Parabel
Die Arbeitsblätter und Lösungsblätter befinden sich nur im Download-Bereich!
Für die beiden Blätter haben wir eine interaktive Geogebra-Answendung erstellt, mit der du die Aufgaben nachvollziehen kannst.
1. Die proportionale Funktion im Intervall 0-1
Der Link zu Geogebra: http://www.geogebratube.org/material/show/id/82376
Verändere mit der Maus die Anzahl n der Intervalle.
2. Die Normalparabel im Intervall 0-1
Der Link zu Geogebra: http://www.geogebratube.org/material/show/id/82373
Verändere mit der Maus die Anzahl n der Intervalle.
Auf den Arbeitsblättern zum Ergänzen der Ober- und Untersummen:
Auf den Lösungsblättern befinden sich die ausführlichen Herleitungen:
