Lineare Funktionen einfach erklärt
Lineare Funktionen verstehen: Zeichnen, Geradengleichung, Steigung, Y-Achsenabschnitt
Das Thema „Lineare Funktionen“ stellt die Schüler in Klasse 7 oder 8 bei der Einführung erstmals vor abstrakte Definitionen und Formalismen, die in dieser Form bisher nicht bekannt waren. Man kann mit Recht sagen, dass ab jetzt das „Rechnen“ ein Ende hat und langsam die „Mathematik“ beginnt. Für die weiteren Themen noch bevorstehenden Klassenstufen ist es daher enorm wichtig, „Lineare Funktionen“ richtig gut zu verstehen!
Das Thema ist für das Gymnasium ebenso wichtig wie für Realschule oder Gesamtschule. Hier schreibt ihr mit Sicherheit mindestens eine Klassenarbeit Lineare Funktionen!
Zu diesem Thema stellen wir daher hier die wichtigsten Begriffe vor.
Darüber hinaus findest du ein abgeschlossenes Skript "lineare Funktionen" mit umfangreichen Aufgaben und Übungen als Ergänzung mit online Zugang.
1. Lineare Funktionen der Einstieg
Zuordnungen
Beispiel 1: Lars kauft beim Obsthändler Walnüsse, das Kilogramm kostet 4 €. Wie viel kosten 200 g, 500g, 1,2 kg? | |
Beispiel 2: In einem Parkhaus kostet das Parken pro angefangener halben Stunde jeweils 1 €. Ab der 2. Stunde kostet die halbe Stunde nur noch 0,75 €. Länger als 4 Stunden Parken kostet pauschal 7,50 €. Berechne jeweils die Parkgebühr für 10min, für 50 min, für 2h 20 min, für 6 h 15 min. | |
Beispiel 3: Zum Frühstück am Sonntag gibt es bei Meyers immer 4-min Frühstückseier. Wie lange dauert es, bis 2, 3, 5 Eier fertig gekocht sind? |
In diesen Beispielen werden immer Werte einander zugeordnet:
- Der Menge der Walnüsse ist der Preis dafür zugeordnet.
- Der Parkdauer ist eine Parkgebühr zugeordnet.
- Den Eiern ist eine Zeitdauer zugeordnet.
Um solche Zuordnungen übersichtlicher darzustellen und um die Fragen zu beantworten, gibt es verschiedene Möglichkeiten. Eine davon ist die Wertetabelle:
Zu Beispiel 1:
kg Walnüsse | 1 kg =1000g | 100 g | 200 g | 500 g = 0,5 kg | 1,2 kg =1200 g |
Preis in € | 4 € | 0,40 € | 0,80 € | 2,00 € | 4,80 € |
Um die gesuchten Preise für 200 g, 500 g und 1,2 kg einfach zu berechnen, ist es hilfreich, zuerst den Preis für eine kleine Menge zu notieren, hier z.B. für 100 g.
Zu Beispiel 2:
Parkdauer | 0,5 h = 30 min | 10 min | 50 min | 2h 20min | 6h 15min |
Parkgebühr | 1 € | 1 € | 1€+1€ = 2 € | 4 x 1€ + 0,75€ = 4,75 € | 7,50 € |
Um die Parkgebühren zu berechnen, ist zu beachten, dass sie sich nicht gleichmäßig verändern, sondern „springen“.
Zu Beispiel 3:
Anzahl Eier | 1 Ei | 2 Eier | 3 Eier | 5 Eier | 10 Eier |
Kochzeit in min | 4 min | 4 min | 4 min | 4 min | 4 min |
Alle Eier werden gleichzeitig fertig!
Die Zuordnungen kann man auch grafisch in einem Schaubild darstellen. Dazu werden die Werte in einem Koordinatensystem eingezeichnet. Man kann dann auch weitere Werte ablesen.
Beispiel 1 - Walnüsse: Was kosten 800 g?

Beispiel 2 - Parkgebühren: Parkgebühr für 1h 15 min?

Beispiel 3 - Eier: Auch 8 Eier benötigen genau 4 Minuten.

Man nennt solche Zuordnungen auch Funktionen. Bei Funktionen ist einem bestimmten x-Wert (z.B. x kg) genau ein y-Wert (z.B. y €) zugeordnet. Im Schaubild werden Funktionen durch entsprechende Linien dargestellt. Diese nennt man Graph der Funktion.
2. Gerade, Steigung, Steigungsfaktor
Im Beispiel mit den Walnüssen erkennt man: wenn doppelt so viele Nüsse (2•x kg) gekauft werden, dann kosten sie doppelt so viel (2•y €). Eine solche Funktion nennt man proportionale Funktion.
Sie wird im Schaubild durch eine Gerade dargestellt, die durch den Ursprung des Koordinatensystems geht.
Diese Gerade kann man mit der Gleichung: y = a • x beschreiben.
Dabei heißt a der Steigungsfaktor oder kurz Steigung. Er wird durch Umformung der Gleichung: a = y/x berechnet.
Der Steigungsfaktor ist das Maß für die Steigung der Geraden im Schaubild.
Beispiel:
Im unserem Beispiel mit den Nüssen entnimmt man der Wertetabelle z.B. x = 1000 (g) und y = 4 (€).
Es ergibt sich für die Steigung:
Also gilt die Gleichung:
Rechenbeispiel: Was kosten 600 g?
Antwortsatz: 600 g Nüsse kosten 2,40 €.
Merke: Zur Bestimmung der Geradengleichung einer proportionalen Funktion kann man den Steigungsfaktor mit zugeordneten Werten aus der Wertetafel berechnen.
Beispiel:
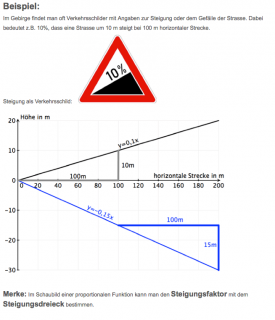
Im Gebirge findet man oft Verkehrsschilder mit Angaben zur Steigung oder dem Gefälle der Strasse. Dabei bedeutet z.B. 10%, dass eine Strasse um 10 m steigt bei 100 m horizontaler Strecke.
Steigung als Verkehrsschild: 

Merke: Im Schaubild einer proportionalen Funktion kann man den Steigungsfaktor mit dem Steigungsdreieck bestimmen.
Weitere Aufgaben auch in der Klassenarbeit zu linearen Funktionen.
Beispiele
Beispiel 1: Die Steigung einer Straße beträgt 10%. Dann ist die Steigung a:

und die Geradengleichung lautet:

Beispiel 2: Das Gefälle einer Straße ist 15%. Also geht es um 15 m bergab, somit ist der y-Wert negativ: - 15. Somit ist die Steigung:

und die Gleichung der Geraden lautet:

Kennt man die Geradengleichung, so kann man das Schaubild mit der Geraden mit Hilfe eines Steigungsdreiecks zeichnen.
Beispiele:
y = -0,5x: gehe 2 nach rechts und 1 nach unten. Die Gerade geht durch die Punkte (0;0) und (2;-1)
y = 3x: gehe 1 nach rechts und 3 nach oben zum Punkt (1;3)
Siehe Bild:
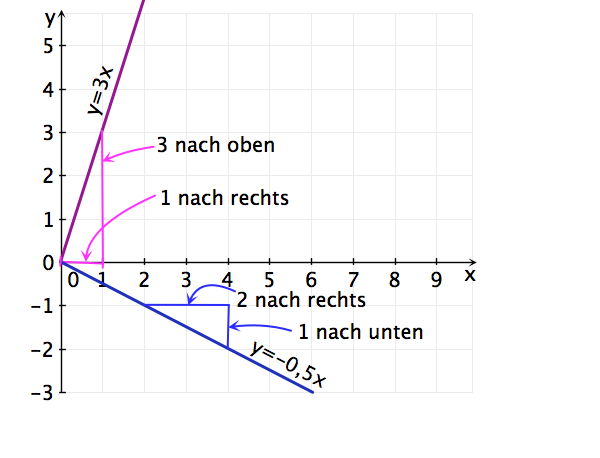
Es gilt immer: gehe einen Schritt nach rechts und dann nach oben (oder unten) zum Punkt auf der Geraden. Der Weg in y-Richtung ist dann der Wert der Steigung!
3. Lineare Funktionen
Einstiegsbeispiel:
Mit ihrem Elektro-Fahrrad kann Nicoletta 40 km weit mit einer Akkuladung fahren. Wenn sie schön gleichmäßig fährt, dann hat sie nach 10 km ein Viertel der Akkuladung verbraucht, also noch für 30 km "Saft". Um das Schaubild dazu zu zeichnen wird zunächst eine Wertetabelle erstellt:
x: Akkuverbrauch | 0 | 1/4 | 1/2 | 3/4 | 1 |
y: mögliche Entfernung | 40 km | 30 km | 20 km | 10 km | 0 km |
Die Punkte liegen alle auf einer Geraden. Die Steigung ergibt sich mit dem Steigungsdreieck:


Die Gerade geht nicht durch den Ursprung des Koordinatensystems, sondern ist nach oben um 40 verschoben. Damit ergibt sich als Geradengleichung:

Eine Funktion mit einer Geradengleichung der Form

heißt lineare Funktion.
Manchmal schreibt man die Geradengleichung auch in der Form:
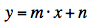
m und n sind hier nur andere Bezeichnungen anstelle von a und b!
Man schreibt auch:


Beispiele:

4. Geradendarstellung: Punkt-Steigungsform, 2 Punkte-Form
Dieses Thema behandeln wir im Skript.